
Today, I’d like to try something and see how it works out. Using the Boids work I did recently as a starting point, I’m wondering if I could get something interesting if I grouped boids into groups of three, and instead of drawing the boids themselves, draw the triangles defined by the positions of each boid in each group of three. I’m not sure how well that will work, but let’s give it a try!
This required very few code modifications to make happen! We still generate the boids the same way, making sure to have a number of boids that is a multiple of three. Then in the view() function, we read the boids out in groups of three, and just draw a triangle using the three boids’ positions.
The boids the form a triangle group are not related. They are just the first three created, the second three, and so on. So, especially in the first few frames, none of those boids are necessarily close to each other. As the app runs, however, the boids flock together. The boids that form any given triangle group may not be in the same flock, and that will change over time as the flocks break up and reform according the rules. The relevant portion of the view() function looks like this:
for group in 0..NUM_BOID_GROUPS {
let i = (group * BOID_GROUP_SIZE) as usize;
let color = model.boids[i].color;
let mut points = Vec::new();
for ip in 0..BOID_GROUP_SIZE as usize {
points.push(model.boids[i + ip].position)
}
draw.polygon()
.color(STEELBLUE)
.points(points.clone())
.color(color);
for ip in 1..BOID_GROUP_SIZE as usize {
draw.line()
.start(points[ip - 1])
.end(points[ip]);
}
draw.line()
.start(points[BOID_GROUP_SIZE as usize - 1])
.end(points[0]);
}
For each group, we get its three points and draw a filled-in polygon using those points. We use the color of the first boid in the group as the fill color. Then using those same points, we draw the outline of the polygon in black. In motion, it looks something like this:
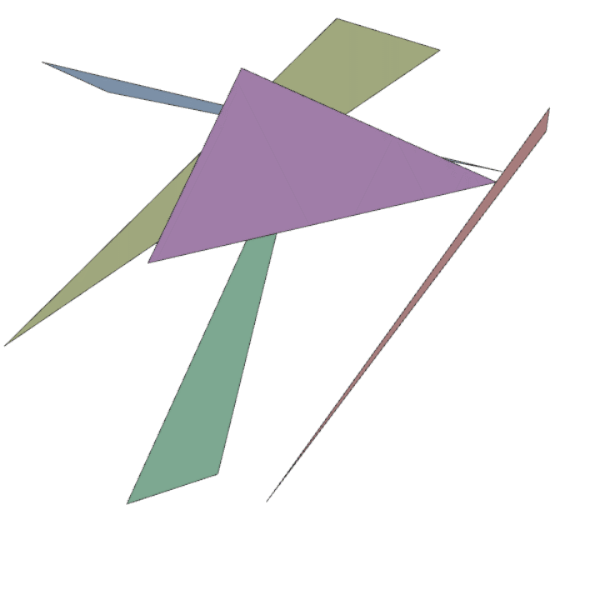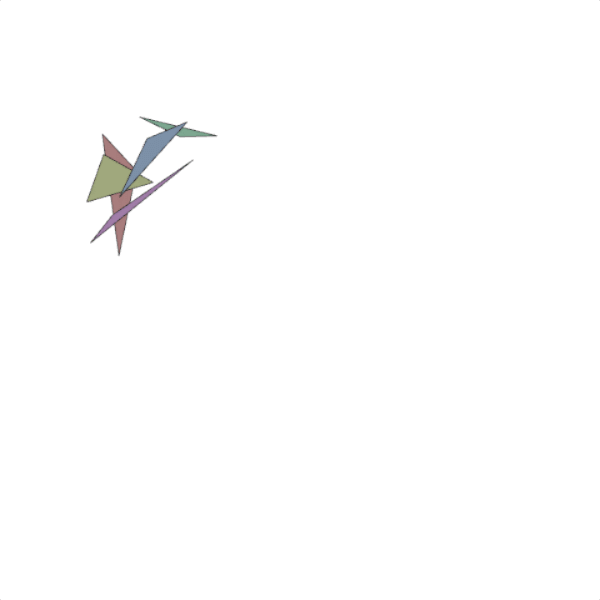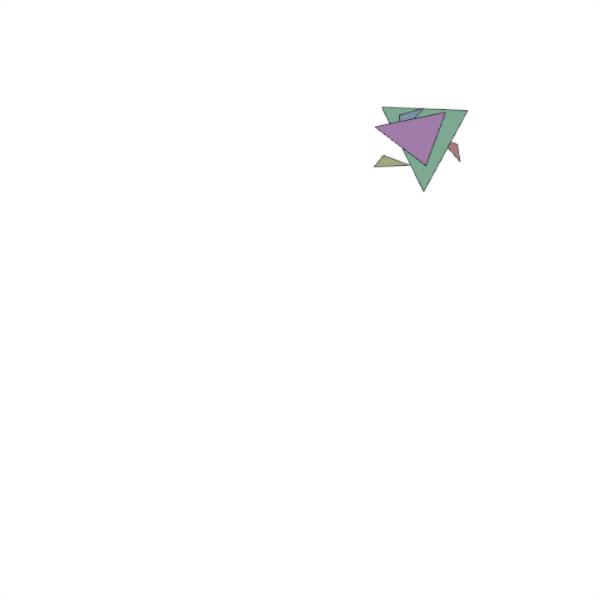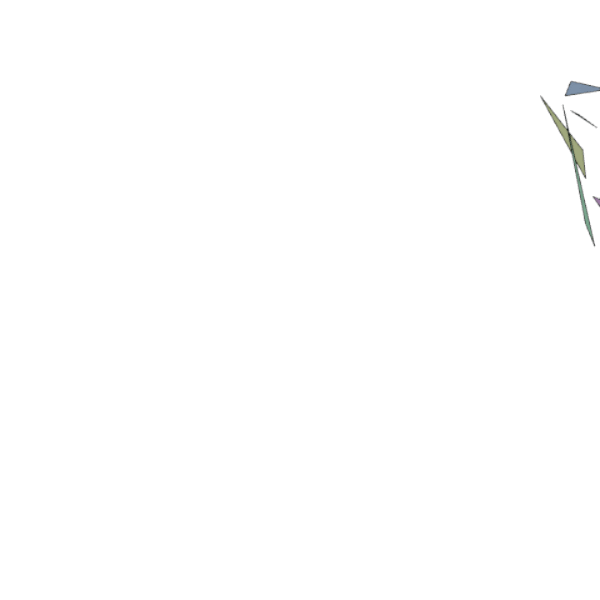
Notice how the vertices of the triangles start far apart, then gather into groups as the boids associated with those points start to flock. With such a small window in this example, and such a small number of boids, this doesn’t get too interesting. Once they have all settled into a single flock, they just start going back on forth. There are a number of things we could do here, but I think I will set this aside for now and ponder how I would like to proceed.
The source code is, as always, in Gitlab .