
Today, we’ll play The Chaos Game! It’s easy to play, and it goes like this:
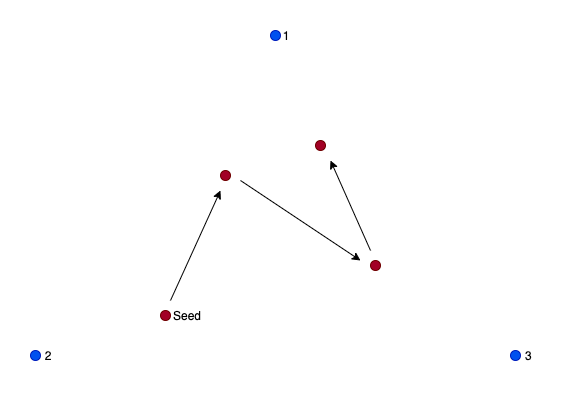
First, put three points on your paper. These will be the vertices of a triangle (so don’t put them in a straight line!) Any triangle will work, but be sure to leave lots of area inside where the triangle will be to make it easier to see what it going on.
Next, you need a way to randomly choose one of those vertices over and over. You can roll a die, and if you get a 1 or a 2, that could reference the first vertex, a 3 or a 4 could reference the second vertex, and a 5 or a 6 could reference that last vertex. If you are a Dungeons and Dragons player and happen to have a 3-sided die, feel free to use that!
Now chose a another point inside the triangle; it doesn’t matter where. Actually, a point outside the triangle also works fine, because you’ll eventually end up inside the triangle anyway. This is called the seed point, and is the starting point for the game.
Here’s where the fun begins! Use your die to choose a vertex at random, and draw a point halfway between the seed point and that vertex. Starting at that new point, randomly choose a another vertex (it could be the same one) and draw another point halfway between your new point and that vertex. Do this an infinite number of times (or until you get tired.)
Can you guess what the final image will look like after a large number of points are added. Probably! You are all smarter than average, and saw the image at the top of the post, so you already have a good idea where this is going. But if you hadn’t seen the image first, could you have guessed that is what you’d end up with?
So why does this set of rules produce this pattern? Look again at the image at the top of this post. Suppose we start with a seed point exactly in the center of the largest white triangle, which also happens to be the center of the overall triangle. That actually is the point I started at when drawing this image, so if you look closely, you can see a dot there. If you choose a vertex at random and find the point halfway between the center and that vertex, you’ll find yourself in the middle of one of the three second-largest white triangles. Sure enough, if you look at the uppermost one closely, you’ll see a dot in the center. From there if you choose a vertex at random, you’ll find youself in the center of one of the third-largest white triangle, and so on.
The large white triangle is there because, as you apply the rules to progressive points, there is no point you can get to where half the distance to any vertex is inside that triangle. The second-largest white triangles are there because each smaller triangular area is similar to the overall area. The visual structure comes from the fact that each successive point goes to a triangle that is half the size of the previous one. In this case, we are printing 50000 points. After about 8 points (at the scale at which we are drawing,) the dot you are making is bigger that the triangle, so subsequent dots just serve to fill in around all those areas that can never be reached.
The Clojure program which does this is surprisingly short:
(ns my_clj.sierpinski
(:require [quil.core :as q]))
(defn midpoint
[[x1 y1] [x2 y2]]
[(/ (+ x1 x2) 2) (/ (+ y1 y2) 2)])
(def vertices
(let [scale 350]
[[0 (- scale)]
[(* scale (q/cos (/ (* 5 Math/PI) 6))) (* scale (q/sin (/ (* 5 Math/PI) 6)))]
[(* scale (q/cos (/ Math/PI 6))) (* scale (q/sin (/ Math/PI 6)))]]))
(def generate-points
(let [seed [0 0]
next #(midpoint % (rand-nth vertices))]
(iterate next seed)))
(defn setup []
(q/background 240)
(q/stroke 100 0 0)
(q/with-translation [(/ (q/width) 2) (/ (q/height) 2)]
(doseq [[x y] (take 50000 generate-points)]
(q/point x y))))
(defn -main [& args]
(q/defsketch sierpinksi
:title "Sierpinski Triangle"
:setup setup
:size [800 800]
:features [:keep-on-top]))
I see by the looks on your faces that this requires some explanation! I completely understand – it took me a while to be able to wrap my head around how to do this!
There is a midpoint function that, when passed two points, will return the point halfway in between them.
There is a vertices variable that defines each vertex of the enclosing triangle. It is effectively a vector (array) of three points.
The generate-points variable requires a bit of explanation. It is a potentially infinite series of points making up the image. What is assigned to that variable is the output of that let function. It sets up the starting point, seed, and another variable called next. next is set to an anonymous function which accepts a parameter. The function, when called, will call the midpoint function with whatever is passed in plus one of the three random vertices. Nothing has happened yet, these are just local variables which have been set up. The meat here is the iterate function which is passed a function to iterate (next) and parameters to that function (seed). iterate generates a sequence created by calling next with seed, adding the result to the sequence, then calling next again with that result as the new seed. This happens over and over again, generating an infinitely long sequence! You are probably wondering how that could be. Where did we get an infinite amount of time to generate that sequence, and where in the heck are we storing it? The key is lazy evaluation. This means that no calculation takes place until something tries to read the sequence. Then as many items as are asked for are generated.
The remaining important part of this program is the setup function, which Quil will call one time. Since we are drawing a static image in this case, that is all we need. This function sets the background and stroke colors. As for the rest of it, the core is the doseq function with takes a sequence of items and does something with each one. The sequence it gets is (take 50000 generate-points), which will be the first 50000 points generated by generate-points. What it does with each point is draw it on the canvas with q/point. The doseq function is wrapped in a q/with-translation function which centers the whole thing on the canvas.
That’s all there is to it!
This is of limited use, however. No matter what starting point I pick, I end up with essentially the same image. I can change the shape of the original triangle, but this is only a superficial change. So what is the point? This is an example of an Iterated Function System (IFS). I plan to use this technique to generate some more complex images in the (hopefully) near future.
By the way, the image we generated here is a Sierpinski Triangle , and is an example of a fractal . An IFS is one of several ways to generate this kind of image, but not at all the only way. Check out the links in these last two paragraphs if you’re interested in learning more!